확률변수란 확률 실험을 통해 얻어지는 기본결과 각각에 수치를 대응시킨 것을 말한다.
따라서 표본공간 S에서 정의된 실함수는 X:S->R 이다.
확률변수의 종류
1. 이산확률변수: 취할 수 있는 가능한 값이 유한개이거나 셀 수 있는 확률변수
-이산확률분포: X가 취할 수 있는 서로 다른 수치를 그것에 대응하는 확률과 함께 적어 놓은 것
ex) 동전던지기 확률분포
| x | H | F |
| f(x) | 1/2 | 1/2 |
-확률질량함수: x의 값을 매개변수로 하여 해당하는 확률 값을 계산하는 함수로써 f(x)=P(X=x) 로 정의된다.
-기댓값:

으로 정의되며 위표에서 앞면이 한번 나올 확률은 0 x 1/2 +1 x 1/2 = 1/2 로 계산된다.
기댓값은 임의의 상수에 대하여 E(ax+b)= aE(x)+b 로 분리된다.
또한 E(X+Y) = E(X) + E(Y)로 분리할 수 있다
-분산과 표준편차:

, 그리고

이산확률분포에서 분산은 제곱의 평균 - 평균의 제곱으로 간단히 계산가능하다.
분산은 임의의 상수에 대하여 Var(aX+b) = a^2Var(X), 표준편차는 sd(aX+b)=|a|sd(X)를 만족한다.
분산과 표준편차는 항상 양의 값을 가지며 상수의 분산은 항상 0이다.
1)베르누이 분포: 계속적으로 반복되어 진행되는 실험을 시행이라고 할 때, 각 시행에서 얻어질 수 있는 기본결과가 단 두 개이면 이러한 시행을 베르누이 실행이라고 한다. 다시 말해 이산확률분포 중 항이 두 개 밖에 없는 것을 의미한다. 따라서 결과는 오직 성공(S)과 실패(F)로 나타난다.
베르누이 확률변수란 베르누이 실행으로 정의된 X(s)=1, X(f)=0인 확률변수 X를 말한다.
위에서 표로 작성한 동전을 한 번 던지는 실험도 베르누이 실행이라고 할 수 있다.
ex) 대학합격/불합격, 불량품/양품,
베르누이 분포는 베르누이 확률변수의 확률 분포를 베르누이 분포라고 할 수 있다.
| x | 0 | 1 |
| p(x) | 1-p | p |
베르누이 분포는 X~B(1, p) 또는 X~B(p)로 표기한다.
베르누이 분포의 평균 E(X) = p (n=시행횟수)로 계산되며 분산 Var = p(1-p) 이다.
2)이항확률변수
베르누이 분포에서 더 나아가 각 시행에서 성공확률이 p인 베르누이 실행을 n번 독립적으로 반복할 때 얻어지는 성공의 횟수 X가 이항분포를 따를 때 X는 이항확률변수라고 부르고 X~B(n,p)으로 표기한다.
확률질량함수는 아래와 같이 계산할 수 있다. n회 시행에서 p확률을 가지는 결과가 x번 등장했으며, 그렇지 않은 결과는 n-x등장했음을 구한다.
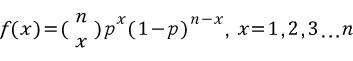
(n x) 는 수학에서 조합을 뜻하며 n개의 표본에서 x를 고르는 조합의 수를 모두 계산한다.
따라서 nCx(=n! / x!(n-x)! 을 구하면 된다.
기대값은 E(X)=np, 분산은 Var(X)=np(1-p)로 정의된다.
예를 들어 동전을 100번 던져서 앞면이 나오는 횟수가 X일 때, X의 기댓값은 100 x 0.5 = 50 이며 분산은 25가 된다.
확률 P(X=x)를 계산할 때는 누적이항확률표를 보고 구할 수 있다. P(x>5) 는 1-(P(x<=4)를 계산하면 된다.
3)기하확률변수: 각 시행에서 성공할 확률이 p인 베르누이 시행을 독립적으로 반복시행할 때 첫 성공을 얻기까지 시행을 하는 횟수를 기하확률변수 X라고 했을 때, X는 기하분포를 따른다.
기하확률분포는 성공이 발생할 때까지는 시행을 계쏙하기 때문에 성공이 일어나기 매우 드문 경우의 발생 비율을 추정할 때 주로 사용한다. 예를 들어 희귀병을 조사하기 위해 마을에서 표본을 추출해서 검사를 했는데 아무도 그 병에 걸린 사람이 없다고 하면 이러한 방법은 효과적이지 못하기 때문에 나타날때까지 검사를 계속하는 것이 바람직하다.
기하분포의 표기는 X~Geo(p)로 하며 확률량함수는
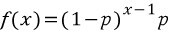
과 같이 계산한다.
성공이 되기전까지의 시행(1-p)을 x번 이전까지 찾을 확률과, 찾을 확률의 곱으로 계산된다.
2. 연속확률변수: 연속적인 구간의 모든 값을 가질 수 있는 확률변수
-연속확률변수는 이산확률변수와 달리 표의 형태로 나타내기 어렵기 때문에 구간으로 나누어 히스토그램으로 그릴 수 있다. 이와같이 도수를 증가시키고, 계급을 무한대로 잘게 나눠가면서 점점 세분화하면 곡선의 그래프가 나타날 것이다.
이러한 곡선을 연속확률변수 X의 확률밀도곡선이라 한다. 그리고 이 곡선을 나타내는 수학적인 함수 f(x)를 연속확률변수 X의 확률밀도함수라 한다.
히스토그램의 특성상 각 상대도수로 이루어진 면적의 총 합은 1이며 음의 확률을 가질 수 없기 때문에,
확률밀도곡선 f(x)은 모든 x에 대해 f(x)>=0 이며, 확률밀도곡선 아래의 면적은 1을 만족한다.
또한 a<X<b사이의 확률은 a~b범위에서 f(x)를 x에 대해 미분한 값이다.
-정규분포: 과거에 모든 통계학 자료는 종 모양의 대칭 형태를 나타내는 것을 발견하여 이를 normal distribution 이라고 명했다.
정규분포는 X~N(μ,∂²)으로 표기한다.
정규분포의 분산은 밀도함수의 모양을 결정하고, 평균은 중심위치를 나타낸다.
표본평균의 경험적 확률과 동일하게 μ±∂ 에 자료의 약 68%를 포함하고, μ±2∂에 약 95%, μ±3∂에 약 99%가 포함된다.
표준 정규분포는 X가 평균이 0, 분산이 1인 정규분포를 따르며, 이를 따르는 확률변수를 주로 Z로 표기한다. Z~N(0,1)
정규분포에서 표준정규분포로 표준화는 다음 관계식을 통해 표준정규분포로 대응시켜서 확률 값을 계산한다.
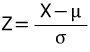
이러한 정규분포의 성질을 이용하면 일반 정규확률변수 X에 대한 확률문제를 표준정규확률 변수 Z의 확률문제로 바꿀 수 있다.

이렇게 계산된 범위는 표준정규분포표를 이용하여 확률을 구한다.
-이항분포의 정규근사: 이항분포의 n이 충분히 크고 p가 0.5에 가까운 경우,
이항확률변수 X는 평균이 np이고 표준편차가 √np(1-p) 인 정규분포에 매우 잘 근사함이 알려져 있다.
이는 근사적으로 표준정규분포를 따른다는 것으로 이 사실을 이용하여 이항확률변수 X에 대한 확률을 표준정규분포를 이용하여 계산할 수 있다.
이 때 주의할 점은 근사 확률을 계산할 때 이산형의 확률 값을 연속형의 표준정규분포로 근사시키는 것이기 때문에 연속성의 수정을 하여야 정밀도를 높일 수 있다. 연속성의 수정이란 이산확률변수 X에 대한 확률 P[X=x]를
P[X=x]=P[x-1/2≤X≤x+1/2]
로 수정하여 계산하는 것을 의미한다. 연속확률변수의 경우 한 값을 취할 확률이 항상 0이기 때문에 이산확률변수의 확률을 얻기 위해서는 1/2를 더하고 빼주어 구간의 형태로 수정한 후 연속확률변수에 대한 확률로 근사시킨다.
이 후에는 평균이 np이고 표준편차가 √np(1-p) 인 사실을 이용하여 정규화를 시켜 표준정규분포표에서 확률 값을 구한다.
'Computer > Statistics' 카테고리의 다른 글
| [기초통계학] 확률 / 조건부 확률 (0) | 2021.11.19 |
|---|---|
| [기초통계학] 중심측도, 변이측도 (표본 / 분산 / 편차 ) (0) | 2021.11.18 |
| [기초통계학] 자료의 요약 방법 (0) | 2021.11.12 |
| [기초통계학] 기본개념 (0) | 2021.11.11 |